Institute for Theoretical Physics, Technical University of Braunschweig

|
Solid-State Theory Division (AG FKT) Institute for Theoretical Physics, Technical University of Braunschweig |
 |
|
Home People Publications Teaching Jobs ITHP TUBS Imprint Privacy |
Electrons have both, charge and spin. Charge is is a quantity known already to classical electrodynamics. Charge transport forms the very basis of our everyday's electric and electronic devices. The electron's spin however, is a purely quantum mechanical object and only today, as the physical device dimensions start to hit the boundaries set by the laws of quantum mechanics, it has become clear that spin currents give rise to completely novel transport phenomena and may introduce a new kind of information technology the so-called spintronics. In this context one of our research efforts is to study spin transport in quantum magnets, which are materials with predominantly localized spin degrees of freedom. 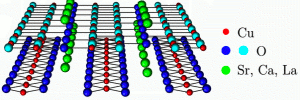 The preceeding figure shows the chemical structure of a prominent member of this class of materials, i.e. an electronically low-dimensional transition metal oxides, the so-called spin-ladder compound (Sr,Ca,La)14Cu24O42. This materials is highly anisotropic and contain localized quantum spin-1/2 magnetic moments which are located on the sites of the blue copper atoms. If biased by a temperature gradient the spin-ladder compounds reveal the remarkable phenomenon of colossal spin heat-transport due to thermal fluctuations of the localized magnetic moments. In fact the magnetic heat current can be shown to flow along the spin ladders with a transport mean free path of more than 700 unit cells. 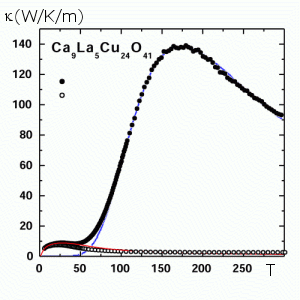 Using various tools of theoretical many-body physics like: Exact diagonalization, Quantum field theory, and Moment expansion, members of the AG-FKT study the current response functions of microscopic quantum mechanical models of transition metal oxides in order to understand the origin of such unconventional transport phenomena. The next figure shows the results of a large scale numerical simulation to determine the finite size scaling of the thermal DC-conductivity, the so-called Drude-weight of a frustrated one-dimensional j1-j2 spin-chain model. 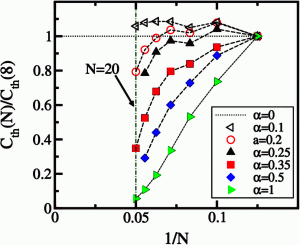 Today there is still far too little understanding of the factors, which might play a role in optimizing and controlling the size of the thermal and other conductivities of such complex systems. Therefore future research faces the continuing challenge to pin down the relevant transport and relaxations channels. Frustration is a new paradigm in statistical
physics which is invoked to understand the intriguing properties of many
novel complex materials. Some of these properties may lead to applications
for storage media, Q-bits, magnetic cooling devices, and quantum switches.
 Inquiring into the possible phases of frustrated magnets is an exciting challenge which members of the AG-FKT pursue with a multitude of tools ranging from methods of quantum field theory to numerical approaches like arbitrary precision series expansion - like in the next figure which proves that the Luttinger liquid of spins on a chain give way to a criss-crossed valence-bond solid if coupled via frustrated inter-chain exchange 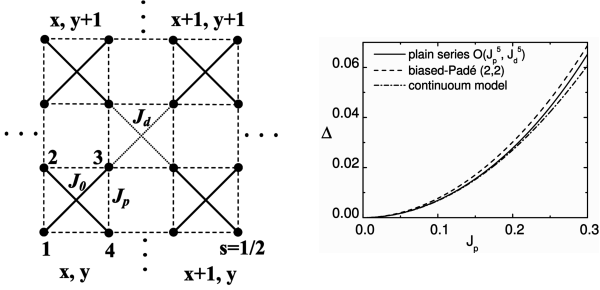 This can be been found by evaluating the of low-lying elementary excitations, the spin gap shown in the right figure. The different phases of matter are intimately connected to our very existence, staring from rather fundamental issues, like the various states of matter following the big bang of the early universe down to the more fun-stuff, like the phases of H2O which make up for ice cream, skiing, ice-climbing, and you-name-it if, ... well, if the temperature drops below the transition temperature Tc of the corresponding phase transition. By now it is well established, that finite temperature phase transitions are governed by universal laws, set by only a few quantities, like the dimension of the physical space and the dimension of the order parameter. Only very recently it has become clear that symmetry changes at zero temperature which are driven by quantum fluctuations and can be tuned by some control parameter, like pressure, magnetic field, or internal coupling constants rather than by temperature, form a novel class of so-called quantum phase-transitions (QPTs). Today QPTs are under intense scrutiny worldwide. They may be a key to the unconventional behavior of many novel materials, since it is believed, that quantum-critical singularities from the absolute zero of temperature will reach up into our real world at finite temperature. QPTs also open the window to new universal behavior and collective dynamics, as well as to fascinating topics like deconfinment or fractionalization of elementary excitations. 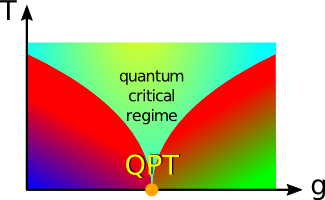 In the AG-FKT we are currently
focussing on QPTs in spin systems, where we investigate high
magnetic-field phenomena, quantum critical scaling properties, and the
impact of disorder on QPTs. Disorder may drastically influence QPTs as can
be seen from one of our large-scale Quantum Monte-Carlo
simulations, evidencing the suppression of a QPT in a particular
two-dimensional dimer magnet (the 2D Kondo necklace) and the appearance of
antiferromagnetism by disorder-induced long-range ordering 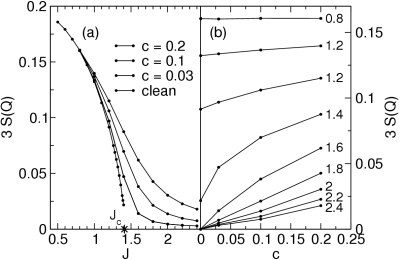 Low Dimensional Quantum Magnets Quantum physics of many particles in one and two dimensions (D) is surprising. Consider electrons, i.e. fermions, of equal spin. In D>1 they can 'somehow' circle around each other to obey Pauli's principle. However, moving in D=1 they have an obvious problem. Looking deeper one finds that fermion and bosons are suddenly more or less the same in D=1, and that long-standing paradigms of condensed-matter physics, like the Fermi-Liquid concept of quasi-particles - which is vital to understanding the interacting many-electron state of metals - break down and allow for new forms of matter like the Tomonaga-Luttinger-Liquid. World-wide progress in material design has provided todays researcher with a multitude of materials in which selected degrees of freedom like spins, orbitals, or charges are dispersing effectively only along one or two dimensions like in the spin-1/2 Heisenberg antiferromagnet chains (HAFC) shown for copper pyrazine dinitrate in the lower left figure. 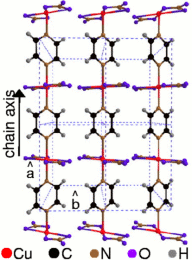  Trying to propagate a single spin-flip (magnon) excitation through such 1D chains forces them to fractionalize into two domain walls (spinons) as shown in the upper left figure. Currently researchers at the AG-FKT use large scale Quantum-Monte Carlo simulations, exact diagonalization and field theoretical tools to inquire into the ground states, thermodynamics, and excitation spectra of such magnets. This is shown for example for the transverse dynamical structure factor of the HAFC, shown below 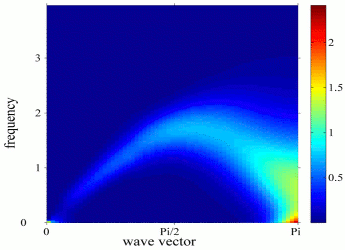 The bright spinon continuum, which is visible in the preceeding figure is a direct consequence of fractionalization. Consider combining the shear endless variations of metallo-organic chemistry's structures with the physics of magnetism. What you get are molecular magnets *, i.e. magnetic materials which range from molecules with only a few magnetic moments to nano-sized clusters with 10-100 magnetic moments up to one-to-three dimensional linked spin networks. These are the focus of a new and highly interdisciplinary research area on the borderline between physics, chemistry, and even bio-medicine. Some typical systems are shown in the following figure * Beware: Chemists can get rather dogmatic about various naming schemes. Physicists tend to have a more relaxed attitude as to what they call a molecular magnet.  Apart from their beautiful structure, molecular magnets show a rich variety of fascinating phenomena, like various mesoscopic quantum oscillation effects, or spin state switching induced by light, presure, or chemical environment. They promise applications in many areas like display design, drug delivery, sensorics and Qbit storage. Using high tempereratue series expansion combined with other tools of many-body physics, members of the AG-FKT have studied thermodynamic properties like the specific heat of metallo-organic 1D ferrimagnets formed from the mixed spin units of systems like MnNi(NO2)4(en)2 (en = ethylenediamine). 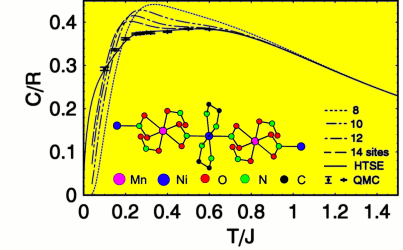 As can be seen, this specific heat develops a characteristic broad shoulder, which is related to the internal excitation spectrum of the mix-spin unit cell. |